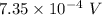Question

An emf is induced in a conducting loop of wire 1.22 m long as its shape is changed from square to circular. Find the average magnitude of the induced emfif the change in shape occurs in 4.25 s and the local 0.125 T magnetic field is perpendicular to the plane of the loop.

Answer 1

The induced emf in the loop is
`7.35* 10^(-4)\ V`

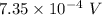
Step-by-step explanation:

Given that,

Length of the wire, L = 1.22 m

It changes its shape is changed from square to circular. Then the side of square be its circumference, 4a = L

4a = 1.22

a = 0.305 m

Area of square,
`A=a^2=(0.305)^2=0.0930\ m^2`

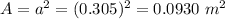
Circumference of the loop,

`C=2\pi r=L\\\\r=(L)/(2\pi)\\\\r=(1.22)/(2\pi)=0.194\ m`

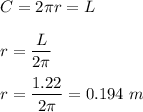
Area of circle,

`A'=\pi r^2\\A'=\pi (0.194)^2\\\\A'=0.118\ m^2`

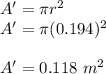
The induced emf is given by :

`\epsilon=(\d\phi)/(dt)\\\\\epsilon=(\d(BA))/(dt)\\\\\epsilon=B(A'-A)/(t)\\\\\epsilon=0.125 * (0.118-0.0930)/(4.25)\\\\\epsilon=7.35* 10^(-4)\ V`

So, the induced emf in the loop is
`7.35* 10^(-4)\ V`