Question

The smallest of the three circles with center D has a radius

of 8 inches and
CB = BA = 4 inches.
What is the sum of the areas of all three circles?
O
80 rt in.
O
96 te in.?
O
20811 in.2
464rt in.

Answer 1

464
`\pi`
`in.^(2)`

Explanation:

did it on edge

Answer 2

The sum of the areas of all three circles is 464
`\pi` squared inches, if the smallest of the three circles with center D has a radius of 8 inches and CB = BA = 4 inches.

Explanation:

The given is,

Three circles,

Smallest circle with center D has a radius of 8 inches.

CB = BA = 4 inches

Step:1

Ref the attachment,

Radius of smallest circle(DC) = 8 inches

Radius of middles circle (DB),

DB = BC + DC = 4 + 8 = 12 inches

Radius of largest circle (DA),

DA = AB + BC + CD = 4 + 4 + 8

DA = 16 inches

Step:2

Formula for area of circle,

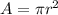`A = \pi r^(2)`.............................(1)

Where, r - Radius of circle

Area of smallest circle,

r = 8 inches

Equation (1) becomes,

`A_(small)` =
`\pi (8)^(2)`

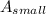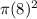
= 64
`\pi`

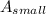`A_(small)` = 64
`\pi` squared inches

Area of middle circle,

r = 12 inches

Equation (1) becomes,

`A_(middle)` =
`\pi (12)^(2)`

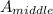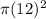
= 144
`\pi`

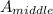`A_(middle)` = 144
`\pi` squared inches

Area of Largest circle,

r = 16 inches

Equation (1) becomes,

`A_(largest)` =
`\pi (16)^(2)`

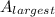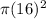
= 256
`\pi`

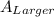`A_(Larger)` = 256
`\pi` squared inches

Step:3

Sum of area of three circles = Area of small circle

+ Area of middle circle + Area of larger circle

= 64
`\pi` + 144
`\pi` + 256
`\pi`

= 464
`\pi` squared inches

Result:

The sum of the areas of all three circles is 464
`\pi` squared inches, if the smallest of the three circles with center D has a radius of 8 inches and CB = BA = 4 inches.