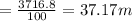Answer:
The height is

Step-by-step explanation:
From the question we are told that
The concentration inside a is tree
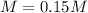
The temperature condition is
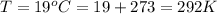
The density of the fluid is
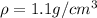
The density of mercury is
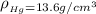
Generally osmotic pressure experience is mathematically represented as
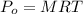
Where R is the universal gas constant with a value of R = 00821 L.atm/K/mol
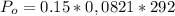
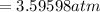
Converting to cm of Mercury
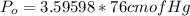
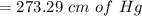
Generally pressure is mathematically represented as
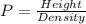
Now making height the subject
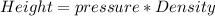
Where pressure is
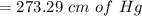
and Density is
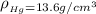
So we have
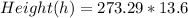
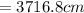
In meters h