Question

A well-known brokerage firm executive claimed that 70% of investors are currently confident of meeting their investment goals. An XYZ Investor Optimism Survey, conducted over a two week period, found that in a sample of 700 people, 74% of them said they are confident of meeting their goals. Test the claim that the proportion of people who are confident is larger than 70% at the 0.05 significance level.

Answer 1

P-value = .010444, this means it is statistically significant or probable that the proportion of people who are confident is larger than 70% at the 0.05 significance level.

Step-by-step explanation:

Population proportion, p = 0.70

Number of people taken in a sample, n = 700

Sample proportion,
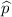`\widehat{p}\\` = 0.74

State the hypotheses:

H ₀:p = 0.70

Hₐ :p < 0.70

one-tailed test, we must calculate z test statistic:

z = (
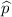`\widehat{p}\\` - p) / √{[p(1 - p)]/n}

z = (0.74 - 0.70) / √{[0.70(1 - 0.70)]/700} = 2.31

z = 2.31

using a table we can find out P-value for Z = 2.31:

P-value = .010444, this means it is statistically significant or probable that the proportion of people who are confident is larger than 70% at the 0.05 significance level.