Question

A study of the pricing accuracy of checkout scanners at a store found that one of every 20 items is priced incorrectly. On any given day, we randomly select five items at a checkout at this store and define X as a variable representing the number of items found to be priced incorrectly by the scanner. a) Assuming that this store sells thousands of items every day, which probability distribution would you use and why? (1 Point) b) What is the probability that exactly one of the five items is priced incorrectly by the scanner? (2 Points) c) What is the probability that at least one of the five items is priced incorrectly by the scanner? (2 Points) Answer.

Answer 1

a) There are going to be at least 15 items both priced correctly, and incorrectly, which means that we can use the normal approximation to the binomial to solve the exercise in this supposed problem.

b) 20.36% probability that exactly one of the five items is priced incorrectly by the scanner

c) 22.62% probability that at least one of the five items is priced incorrectly by the scanner

Explanation:

For each item, there are only two possible outcomes. Either it is priced correctly, or it is not. The probability of an item being priced incorrectly is independent of other items. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

Five items selected.

This means that
`n = 5`

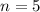
One of 20 is priced incorrectly.

This means that
`p = (1)/(20) = 0.05`

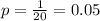
a) Assuming that this store sells thousands of items every day, which probability distribution would you use and why?

There are going to be at least 15 items both priced correctly, and incorrectly, which means that we can use the normal approximation to the binomial to solve the exercise in this supposed problem.

b) What is the probability that exactly one of the five items is priced incorrectly by the scanner?

This is P(X = 1).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 1) = C_(5,1).(0.05)^(1).(0.95)^(4) = 0.2036`

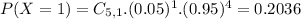
20.36% probability that exactly one of the five items is priced incorrectly by the scanner

c) What is the probability that at least one of the five items is priced incorrectly by the scanner?

Either no items are priced incorrectly, or at least one is. The sum of the probabilities of these events is decimal 1. So

`P(X = 0) + P(X \geq 1) = 0`

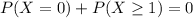
We want
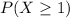`P(X \geq 1)`. So

`P(X \geq 1) = 1 - P(X = 0)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(5,0).(0.05)^(0).(0.95)^(5) = 0.7738`

`P(X \geq 1) = 1 - P(X = 0) = 1 - 0.7738 = 0.2262`

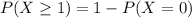
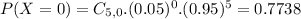
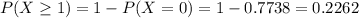
22.62% probability that at least one of the five items is priced incorrectly by the scanner