Question

onsider the equation 0.5 times e4z =13 solve the equation for z. express the solution as a logarithm in base e

Answer 1

`z=(ln(26))/(4)`

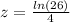
Explanation:

The given equation is:

`0.5\,e^(4z)=13`

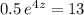
so, we first isolate the exponential form that contains the unknown "z" in the exponent, by dividing both sides by 0.5:

`0.5\,e^(4z)=13\\e^(4z)=(13)/(0.5)\\e^(4z)=26`

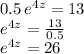
Now we bring the exponent down by applying the natural log function on both sides, and then solve for "z":

`e^(4z)=26\\ln(e^(4z))=ln(26)\\4\,z=ln(26)\\z=(ln(26))/(4)`