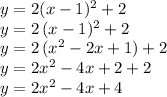Writing quadratics// vertex: (1, 2); passes through (3.10)

Question

asked Apr 4, 2021 27.1k views

1 Answer

Alexey Shevelyov · Answer 1 · 2021-04-09T04:28:35+0000

Answer:

Equation for the quadratic in vertex form:
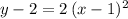
$y-2=2\,(x-1)^2$

Equation in standard form:
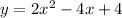
y=2x^2-4x+4

Explanation:

Recall that there is a form for writing the general equation of a parabola in vertex form:

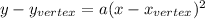
y-y_(vertex)=a(x-x_(vertex))^2

so in our case, considering the the coordinates of the vertex (1,2) are given, we have:

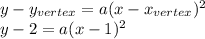
$y-y_(vertex)=a(x-x_(vertex))^2\\y-2=a(x-1)^2$

Now, we can find the parameter "a" missing for the general equation, by using the information on a point (3,10) through which the parabola passes:

$y-2=a\,(x-1)^2\\(10)-2=a],(3-1)^2\\8=a\, (2)^2\\8=4\,a\\a=2$

So now we have the general form of this quadratic:

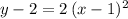
$y-2=2\,(x-1)^2$

which solving for "y" in order to give its standard form results in:

$y=2(x-1)^2+2\\y=2\,(x-1)^2+2\\y=2\,(x^2-2x+1)+2\\y=2x^2-4x+2+2\\y=2x^2-4x+4$