Answer:
The bird's path forms an angle of 9.3° with the first (driving east) road and an angle of 80.7° with the second (driving north) road
Explanation:
Let
A ----> Pottstown
C ----> Cogsville
B ----> the intersection of the two roads
In this problem we have that the two roads are perpendicular
(Remember that North and East are perpendicular axis)
so
see the attached figure to better understand the problem
we know that
The path that a bird could fly in a straight line from Pottstown to Cogsville is the segment AC
so
Find the measure of angle A
In the right triangle ABC
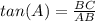 ----> by TOA (opposite side divided by the adjacent side)
----> by TOA (opposite side divided by the adjacent side)
substitute the given values
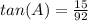
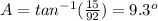
Find the measure of angle C
In the right triangle ABC
we know that
The sum of the angle A and the measure of angle C is 90 degrees , because are complementary angles
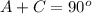
we have
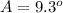
substitute
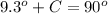
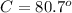
therefore
The bird's path forms an angle of 9.3° with the first (driving east) road and an angle of 80.7° with the second (driving north) road