Question

According to a recent study of 7335 young people in the US, 30% had been arrested for a crime other than a traffic violation by the age of 23. crimes included such things as vandalism, underage drinking, drunken driving, shoplifting, and drug possession.From a study in USA Today, quoted in The Week, 2012; 11: 547-548.(a) Is the 30% a parameter or a statistic?(A) Parameter.(B) Statistic.(b) The margin of error for the population proportion estimate, P, is 0.01. use this information to give a range of plausible values for the parameter

Answer 1

a) Statistic.

b) The population proportion is expected to be between 0.29 and 0.31 with a 94% degree of confidence.

Explanation:

a) The proportion of 30% is a statistic, as it is a value that summarizes data only from the sample taken in the study from USA Today. Other samples may yield different proportions.

b) We can use the statistic to estimate a confidence interval for the parameter of the population.

The standard error for the proportion is calculated as:

`\sigma_p=\sqrt{(p(1-p))/(N)}=\sqrt{(0.3\cdot 0.7)/(7335)}=√(2.83\cdot10^5)= 0.00535`

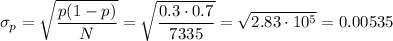
The margin of error is 0.01. We can use this value to determine the level of confidence that represents.

The formula for the margin of error is:

`E=z\cdot \sigma_p=0.01\\\\z\cdot 0.0535=0.01\\\\z=1.87`

This z-value, according to the the standard normal distribution, corresponds to a confidence interval of 94%.

The interval for this margin of error is:

`p-E\leq \pi \leq p+E\\\\0.30-0.01\leq \pi \leq 0.30+0.01\\\\0.29\leq \pi \leq 0.31`

Then, we can conclude that the population proportion is expected to be between 0.29 and 0.31 with a 94% degree of confidence.