Question

A mass attached to the end of a spring is oscillating with a period of 2.25 s on a horizontal frictionless surface. The mass was released from rest at t = 0 from the position x = 0.0700 m.(a) Determine the location of the mass at t = 5.31 s?(b) Determine if the mass is moving in the positive or negative x direction att = 5.31 s?

Answer 1

`x(5.31)\approx -0.0446m`

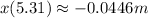
The mass is moving in the negative x direction

Step-by-step explanation:

In a spring mass system, the position of the mass for every time
`t` is defined by:

`x(t)=Acos(\omega t+ \phi)\\\\Where:\\\\A= Elongation\hspace{3} or\hspace{3} displacement\hspace{3} with\hspace{3} respect\hspace{3} to\hspace{3} the\hspace{3} equilibrium\hspace{3} point.\\\omega= Angular\hspace{3}frequency\\t=Time\\\phi=Initial\hspace{3} phase \hspace{3}angle`

The oscillation frequency can be written as:

`f=(\omega)/(2\pi )`

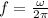
And, since the period is the reciprocal of the frequency:

`T=(2\pi)/(\omega)`

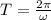
Using the previous equations and the data provided by the problem:

`A=0.0700m\\\\\omega=(2\pi)/(T) =(2\pi)/(2.25)=(8\pi)/(9) \approx2.79\\\\\phi=0`

Therefore:

`x(t)=0.07cos(((8 \pi)/(9) )t )`

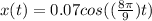
Evaluating t=5.31 into the motion equation:

`x(5.31)=0.07cos(((8 \pi)/(9) )(5.31))=0.07cos((118\pi)/(25))\approx-0.0446m`

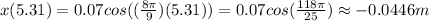
Since the position for t=5.31 is negative, we can conclude that the mass is moving in the negative x direction.