Question

In section 1.1.1.3 we obtained an equation (1.1.26) that described the dynamic behavior of the load shaft speed as a function of the motor input voltage. starting from this equation, find the transfer function ωl(s) . vm (s)

Answer 1

Answer:The required transfer function is ,

`\frac{Kt}{La*Jm*s{2} +(Ra*Jm+Bm*La)*s+(Kt*Ke+Ra*Bm)]}`

Explanation:

Given:

Consider a DC motor

To Find :

Transfer function of load shaft and Input voltage.

Solution:

(Refer the attachment because this website dont allows the some words and so written on paper )

`Ea(t)=Ra*Ia(t)+L*dIa(t)/dt+Eb(t)`............Equation(1)

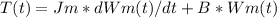`T(t)=Jm*dWm(t)/dt+B*Wm(t)`............................Equation(2)

i.e. Electrical -mechanical equations we get,

E=K*Wm(t)

T(t)=Kt*Ia(t)...................... [ t is used since function are in Time domain]

Taking Laplace transform equation (1) and (2) we get ,

For Electrical,

`Ia(s)=[1/L*s+Ra][Ea(s)-Eb(s)].`.......................(Frequency domain)

For mechanical ,

`T(s)=[Jm*s+Bm]Wm(s)`

And we know that

`T(s)=Kt*Ia(s)`

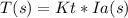
And,

`Wm(s)=[1/(Jm*s+Bm)]*T(s)`

And also

`Eb(s)=Ke*Wm(s)`

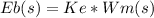
By definition of transfer function:

T.F.= G(s)/[(1+H(s)*G(s)]

`Here is G(s)=Kt*[1/L*s+Ra]*[1/(Jm*s+Bm)]`

Using G(s) value in transfer function we get as ,

Wm(s)/Ea(s)=[
`\frac{Kt}{La*Jm*s{2} +(Ra*Jm+Bm*La)*s+(Kt*Ke+Ra*Bm)]}`

This is required transfer function