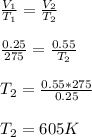Question

A monatomic ideal gas initially fills a container of volume V = 0.25 m3 at an initial pressure of P = 250 kPa and temperature T = 275 K. The gas undergoes an isobaric expansion to V2 = 0.55 m3 and then an isovolumetric heating to P2 = 760 kPa.

Answer 1

number of moles = 27.34 moles

the temperature of gas after it undergoes the isobaric expansion = 605 K

Step-by-step explanation:

Given that:

V = 0.25 m³

P = 250 kPa

T = 275 K

V₂ = 0.55 m³

P₂ = 760 kPa

a)

Using ideal gas equation ; PV = nRT

`n = (PV)/(RT)\\\\n = (250*10^3*0.25)/(8.314*275)\\\\n = (62500)/(2286.35)\\\\n = 27.34 \ moles`

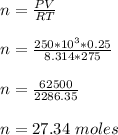
b) To calculate the temperature of gas after it undergoes the isobaric expansion; we have:

1. 
   `(V_1)/(T_1)= (V_2)/(T_2)\\\\(0.25)/(275)= (0.55)/(T_2)\\\\T_2=(0.55*275)/(0.25)\\\\T_2 = 605 K`