Question

Let​ T: set of real numbers R squaredright arrowset of real numbers R squared be a linear transformation such that Upper T (x 1 comma x 2 )equals(x 1 plus x 2 comma 2 x 1 plus 4 x 2 ). Find x such that ​T(x​)equals(3 comma negative 2 ).

Answer 1

The pair (7,-4) maps to the pair (3,-2) under T.

Explanation:

We are given that
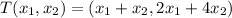`T(x_1,x_2) = (x_1+x_2, 2x_1+4x_2)`. The questions asks for the pair (x,y) such that T(x,y) = (3,-2). So, knowing the behaviour of the transformation T, we know that

T(x,y) = (x+y, 2x+4y) = (3,-2). So, we have the following equations

`x+y =3`

`2x+4y=-2`

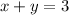
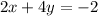
From first equation, we have that x = 3-y. REplacing this result in the second equation, we have that

`2(3-y)+4y = 6+2y = -2`

Which implies that y = -4. Then, x=3-(-4) = 7.