Answer:
a) Therefore 92.64% of customers receive the service for half-price.
b) Therefore it would take 8.52 minutes
Explanation:
Given that ime required for an automotive center to complete an oil change service on an automobile approximately follows a normal distribution with:
mean (μ) = 15 minutes
Standard deviation (σ) = 3.5 minutes
a) The z score is given by the equation:

Since the service will take no longer than 20 minutes,
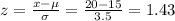
Using the probability table to get the probability of the z score
percent of customers receive the service for half-price = P(X < 20) = P(z < 1.43) = 0.9236 = 92.64%
Therefore 92.64% of customers receive the service for half-price.
b) Since the probability is 3% = 0.03, this corresponds with a z score of -1.88
Therefore:
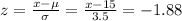
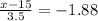
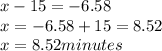
Therefore it would take 8.52 minutes