To solve this problem we will apply the concepts of acceleration according to the laws of kinetics. Acceleration can be defined as the change in velocity per unit time, that is,
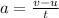
Here,
v = Final velocity
u = Initial velocity
t = Time
Rearranging to find the initial velocity,

Now the acceleration is equal to the gravity, then,
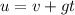
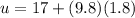
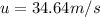
The velocity of the shell at 5.5s after the launch is,
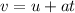
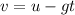
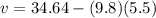
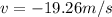
Therefore the magnitude of the velocity of the shell at 5.5s is -19.26m/s