Question

At a point 400 feet from the base of a building, the angle of elevation to the top of the building is 60◦. Find the height of the building (leave your answer in radical form)

Answer 1

The height of the building is 400√3

Explanation:

Given:

Angle of elevation to the top of the building = 60°

Distance from the observer to the base of it = 400 ft

We have to find the height of the building.

Let the height of the building be "h" ft

Using trigonometric ratio:

⇒
`tan(\theta)=(opposite)/(adjacent)`

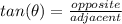
So,

Considering adjacent side as 400 ft.

⇒
`tan(\theta) =(h)/(400)`

⇒
`h=tan(\theta)* 400`

⇒
`h=tan(60)* 400`

⇒
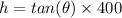
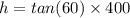
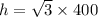`h=√(3) * 400` ...tan(60) = √3

⇒
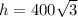`h=400√(3)` ft

The height of the building is 400 Sq-rt (3) ft in terms of radical form and in decimals it is 692.8 ft.