Question

At a carnival, 700 tickets were sold for a total

amount of $5.500. An adult ticket cost $10

and a children's Icket cost $5. Find the

number of adult tickets (x) and the number of

children's lickets (y) sold.

Answer 1

The adult tickets are 400 and the children tickets are 300.

Explanation:

Given:

At a carnival, 700 tickets were sold for a total amount of $5500. An adult ticket cost $10 and a children's ticket cost $5.

Now, to find the number of adult tickets and the number of children's tickets sold.

Let the number of adult tickets be
`x.`

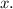
And let the number of children tickets be
`y.`

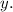
So, the total number of tickets sold:

`x+y=700\\\\y=700-x\ \ \ ....(1)`

Now, the total amount of tickets:

`x(10)+y(5)=5500`

Substituting the value of
`y` from equation (1):

`x(10)+(700-x)(5)=5500\\\\10x+3500-5x=5500\\\\5x+3500=5500`

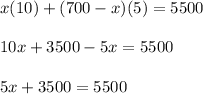
Subtracting both sides by 3500 we get:

`5x=2000`

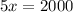
Dividing boths sides by 5 we get:

`x=400.`

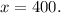
The number of adult tickets = 400.

Now, substituting the value of
`x` in equation (1) we get:

`y=700-x\\\\y=700-400\\\\y=300.`

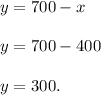
The number of children tickets = 300.

Therefore, the adult tickets are 400 and the children tickets are 300.