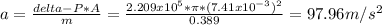Answer:
The initial acceleration is 97.96 m/s²
Step-by-step explanation:
Given data:
m = mass of metal cylinder = 0.389 kg
r = radius of plastic tube = 7.41 mm = 7.41x10⁻³m
P₀ = pressure = 1 atm = 1.013x10⁵Pa
The pressure inside the tube is:
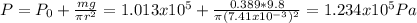
The pressure applied by the plunger is:
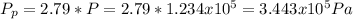
The difference between the pressure applied by the plunger and the pressure inside the tube is:

The initial acceleration is: