Question

4 identical coins of mass M and radius R are placed in a square, so the center of each coin lies on a corner of the square. The coins are touching and stuck to each other. What is the moment of inertia of the system about an axis through the center of the square? Consider the parallel axis theorem, and treat coins as disks of uniform mass.

Answer 1

The moment of inertia for the 4 coins is 10*MR²

Step-by-step explanation:

According the attached diagram, the moment of inertia in point O is:

`I_(O) =(1)/(2) MR^(2)`

The moment of inertia in point A is:

`I_(A) =(1)/(2) MR^(2) +M(OA)^(2) \\OA=(1)/(2) √(2) BO=(1)/(2) √(2)(2R)=√(2) R\\I_(A)=(1)/(2) MR^(2)+2MR^(2) =(5)/(2) MR^(2)`

The, for the 4 coins the moment of inertia is:

`I_(4c) =4*I_(A) =4*(5)/(2) MR^(2) =10MR^(2)`

Answer 2

I_{total} = 10 M R²

Step-by-step explanation:

The concept of moment of inertia in rotational motion is equivalent to the concept of inertial mass for linear motion. The moment of inertia is defined

I = ∫ r² dm

For body with high symmetry it is tabulated, in these we can simulate them by a solid disk, with moment of inertia for an axis that stops at its center

I = ½ M R²

As you hear they ask for the moment of energy with respect to an axis parallel to the axis of the disk, we can use the theorem of parallel axes

I =
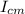`I_(cm)` + M D²

Where I_{cm} is the moment of inertia of the disk, M is the total mass of the system and D is the distance from the center of mass to the new axis

Let's apply these considerations to our problem

The moment of inertia of the four discs is

I_{cm} = I

I_{cm} = ½ M R²

For distance D, let's use the Pythagorean Theorem. As they indicate that the coins are touched the length of the square is L = 2R, the distance from any spine to the center of the block is

D² = (R² + R²)

D² = R² 2

Let's calculate the moment of inertia of a disk with respect to the axis that passes through the center of the square

I = ½ M R2 + M R² 2

I = 5/2 M R²

This is the moment of inertia of a disc as we have four discs and the moment of inertia is a scalar is additive, so

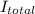`I_(total)` = 4 I

I_{total} = 4 5/2 M R²

I_{total} = 10 M R²