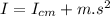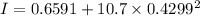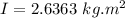Question

In a physics lab, Asha is given a 10.7 kg uniform rectangular plate with edge lengths 67.3 cm by 53.5 cm . Her lab instructor requires her to rotate the plate about an axis perpendicular to its plane and passing through one of its corners, and then prepare a report on the project. For her report, Asha needs the plate's moment of inertia ???? with respect to given rotation axis. Calculate ???? .

Answer 1

`I=2.6363\ kg.m^2`

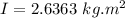
Step-by-step explanation:

Given:

dimension of uniform plate,
`(0.673* 0.535)\ m^2`

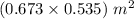
mass of plate,
`m=10.7\ kg`

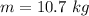
Now we find the moment of inertia about the center of mass of the rectangular plate is given as:

`I_(cm)=(1)/(12) * m(L^2+B^2)`

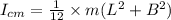
where:

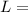`L=` length of the plate

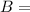`B=` breadth of the plate

`I_(cm)=(1)/(12) * 10.7*(0.673^2+0.535^2)`

`I_(cm)=0.6591\ kg.m^2`

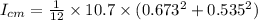
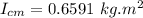
We know that the center of mass of the rectangular plane is at its geometric center which is parallel to the desired axis XX' .

Now we find the distance between the center of mass and the corner:

`s=(√( (0.673^2+0.535^2)))/(2)`

`s=0.4299\ m`

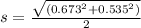
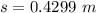
Now using parallel axis theorem:

`I=I_(cm)+m.s^2`

`I=0.6591+10.7* 0.4299^2`

`I=2.6363\ kg.m^2`