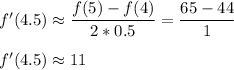Question

In order to measure the flow rate of water coming out of a tap, you can place a bucket under the tap and measure the volume in the bucket as a function of time. The tabulated date given below represents the volume of the water as a function of time. Use the centered-difference formula to estimate the flow rate at t equals 4.5

time 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
volume 0 2 5 9 14 20 27 35 44 54 65 77 90

Answer 1

The flow rate at t=4.5 is approximately 11.

Explanation:

We have tabulated data that relates volume V with time t.

We are asked to determine the rate of flow (variation of volume in time, first derivative dV/dt) at t=4.5.

The centered-difference formula let us calculate an approximation of the first derivative of a function at a specific point, from the values of the function:

`f'(x)\approx(f(x+h)-f(x-h))/(2h)`

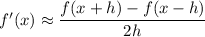
The value of x in this case is 4.5, as it is the point in which we want to calculate the rate of flow.

The value of h is the step used in the table. In this case, h=0.5.

Then the values we need from the function are:

`f(x+h)=f(4.5+0.5)=f(5)=65\\\\f(x-h)=f(4.5-0.5)=f(4)=44`

We now can calculate the first derivative approximation with the centered-difference formula

`f'(4.5)\approx(f(5)-f(4))/(2*0.5)=(65-44)/(1)\\\\f'(4.5)\approx11`