Question

In a lab experiment, a proton is shot directly to the right at 50,000 m/s towards another proton. After the collision, the first proton (the one initially moving) moves at an angle of 30° with respect to the +x axis at a speed of 43,300 m/s. Assuming an elastic collision, what is the velocity (magnitude and direction) of the second proton? Hint: Linear momentum is not the only conserved quantity in an elastic collision

Answer 1

v2'=14435.02 m/s

Step-by-step explanation:

Linear momentum and energy must conserve before and after the collision:

`p_b=p_a\\E_b=E_a\\`

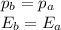
by taking into account both x and y component of the linear momentum we have:

`m_pv_1=m_pv'_1cos(30\°)+m_pv'_2cos(\alpha)\\\\0=m_pv'_1sin(30\°)+m_pv'_2sin(\alpha)`

Where v1, v2, v1' and v2' are velocities of the first and second proton before and after the collision respectively. mp is the mass of the proton.

For the kinetic energy we have:

`(1)/(2)m_pv_1^2=(1)/(2)m_pv'_1^2+(1)/(2)m_pv'_2^2`

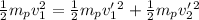
by replacing in the first and second equation equation we obtain:

`v'_2cos(\alpha)=v_1-v_1'cos(30\°)=(50000(m)/(s))-(43300(m)/(s))cos(30\°)=12501.1(m)/(s)\\\\v_2'sin(\alpha)=v_1'sin(30\°)=(43300(m)/(s))sin(30\°)=21650(m)/(s)`

by dividing these equations we get:

`(v_2'sin(\alpha))/(v_2'cos(\alpha))=(21650)/(12501.1)\\\\tan(\alpha)=1.731\\\\\alpha=tan^(-1)(1.731)59.69\°\approx60\°`

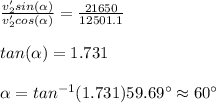
Finally, by replacing in some of the equations for v2':

`v_2'cos(30\°)=12501.1\\\\v_2'=(12501.1)/(cos(30\°))=14435.02(m)/(s)`

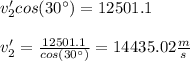
hope this helps!!