Question

A research scholar wants to know how many times per hour a certain strand of virus reproduces. The mean is found to be 13.7 reproductions and the population standard deviation is known to be 2. If a sample of 205 was used for the study, construct the 80% confidence interval for the true mean number of reproductions per hour for the virus. Round your answers to one decimal place.

Answer 1

The 80% confidence interval for the true mean number of reproductions per hour for the virus.

(13.52 , 13.87)

Explanation:

Explanation:-

The mean is found to be 13.7 reproductions and the population standard deviation is known to be 2

the mean of the sample x⁻ = 13.7

The standard deviation of population σ = 2

Given sample size n =205

The 80% of confidence intervals:-

`( x^(-) - Z_(\alpha ) (S.D)/(√(n) ) , x^(-) + Z_(\alpha )(S.D)/(√(n) ) )`

`( 13.7 -1.28(2)/(√(205) ) , 13.7 + 1.28(2)/(√(205) ) )`

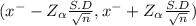
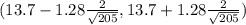
(13.52 , 13.87)

Conclusion:-

the 80% confidence interval for the true mean number of reproductions per hour for the virus.

(13.52 , 13.87)