Question

Triangle F G E is shown. Angle F E G is a right angle. The length of hypotenuse F G is 18.6 inches and the length of F E is 12 inches. Angle F G E is x. Which is the best approximation for the measure of angle EGF? 32.8° 40.2° 49.8° 57.2°

Answer 1

40.2 is correct

Explanation:

Answer 2

Measure of ∠FGE is 40.2°.

Explanation:

Refer to the attachment.

Consider ΔFGE. Given that ∠FEG = 90° and ∠FGE is x°.

To find the value of ∠FGE use trigonometric ratios.

Use sine ratio to find the value of ∠FGE.

`\sin \theta=(opposite\:side)/(hypotenuse\:side)`

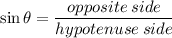
Rewriting it in terms of x° as follows,

`\sin x=(opposite\:side)/(hypotenuse\:side)`

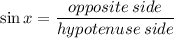
Now find the opposite and hypotenuse side of the angle ∠FGE.

So opposite side of ∠FGE is FE and hypotenuse side of ∠FGE is FG.

Substituting the values,

`\sin x=(FE)/(FG)`

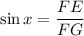
Given that length of FE is 12 inch and FG is 18.6 inch.

Substituting the value,

`\sin x=(12)/(18.6)`

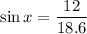
To find the value of x, taking inverse sin.

`x=\arcsin \left((12)/(18.6)\right)`

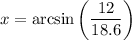
Calculating the value,

`x=40.17`

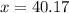
Rounding to nearest tenth the value of angle is 40.2

Therefore measure of ∠FGE is 40.2° .