Question in proper order
The rotational kinetic energy term is often called the kinetic energy in the center of mass, while the translational kinetic energy term is called the kinetic energy of the center of mass.
You found that the total kinetic energy is the sum of the kinetic energy in the center of mass plus the kinetic energy of the center of mass. A similar decomposition exists for angular and linear momentum. There are also related decompositions that work for systems of masses, not just rigid bodies like a dumbbell.
It is important to understand the applicability of the formula
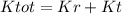
Which of the following conditions are necessary for the formula to be valid?
a. The velocity vector
must be perpendicular to the axis of rotation
b.The velocity vector
must be perpendicular or parallel to the axis of rotation
c. The moment of inertial must be taken about an axis through the center of mass
Answer:
Option c
Step-by-step explanation:
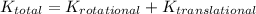
The first two conditions are untrue, this is because, you can have rotation in any direction and translation in any direction of any collection of masses. Rotational and translational velocities of masses do not depend on each other
The last statement is true because by definition, the moment of inertia, which is a measure of reluctance, is usually taken about a reference point which is the center of mass