Answer:
The East Coast confidence interval will be more precise, since the sample is larger.
Explanation:
The margin of a confidence interval is given by the following formula:
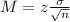
In which z is the critical value related to the confidence level,
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
The larger n is, the lesser the margin of error is, that means that we have a more precise interval.
In this problem:
West Coast: 41 people
East Coast: 121 people
Both 95% confidence interval, so same z. Both about the amount of newly discovered antibody in human blood, so the standard deviation of the population will be the same.
The East Coast has a larger sample. So
The East Coast confidence interval will be more precise, since the sample is larger.