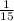Given:
Given that there are 10 marbles in a bag. 4 are blue, 3 are black, 2 are white and 1 is red.
The marbles are selected by not replacing the drawn ones.
We need to the probability of selected a black marble and then a white marble without replacement.
Probability:
Let B denote the black marble.
Let W denote the white marble.
The probability of selecting a black marble is
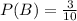
The probability of selecting a white marble without replacement is
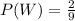
The probability of selecting a black marble and then a white marble without replacement is given by
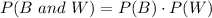
Substituting the values, we get;
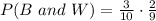
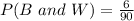
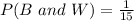
Thus, the probability of selecting a black marble and then a white marble without replacement is