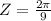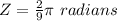Answer:
The angular distance in revolution is
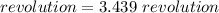
The angular distance in radians is
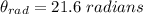
The angular distance in degrees is
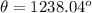
The angular size is
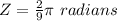
Step-by-step explanation:
From the question we are told that
The diameter is
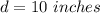
The distance moved by the rim is
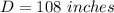
Generally the circumference of the pie plate is mathematically represented as
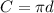
Substituting the values
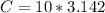
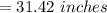
The number resolution carried out by the pie plate is evaluated as

Substituting value
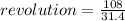
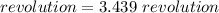
The angular distance
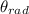 is mathematically evaluated as
is mathematically evaluated as
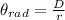
Where r is the radius which is mathematically evaluated as
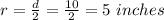
Substituting this into the equation for angular distance
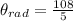
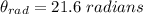
The angular distance traveled in degrees is
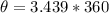
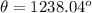
When the pie is cut into 9 equal parts
The angular size would be mathematically evaluated as