Question

Worth 60 points

Consider the following system of equations:
y = -x + 2
y = 3x + 1
Which description best describes the solution to the system of equations?
Line y = -x + 2 intersects line y = 3x + 1
Lines y = -x + 2 and y = 3x + 1 intersect the x-axis.
Lines y = -x + 2 and y = 3x + 1 intersect the Y-axis
Line y = -x + 2 intersects the origin

Answer 1

Line y = -x + 2 intersects line y = 3x + 1

Explanation:

The solution to a system of equations is the point at which the two lines intersect. To find this point, first equate the equations and solve for x:

`\begin{aligned}y & = y\\-x + 2 & = 3x + 1\\-x+2+x & = 3x+1+x\\2 & = 4x + 1\\2-1 & =4x+1-1\\1 &=4x\\x & =\frac14\end{aligned}`

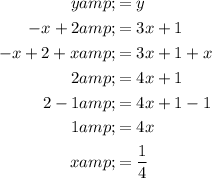
Substitute the found value of x into one of the equations, and solve for y:

`y=3\left(\frac14\right)+1=\frac74`

Therefore, the solution to the system of equations (the point at which the two lines intersect) is:

`\left(\frac14,\frac74\right)`

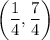
So the description that best describes the solution to the system of equations is:

Line y = -x + 2 intersects line y = 3x + 1