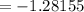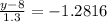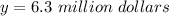Question

Suppose that the quarterly sales levels among health care information systems companies are approximately normally distributed with a mean of million dollars and a standard deviation of million dollars. One health care information systems company considers a quarter a "failure" if its sales level that quarter is in the bottom of all quarterly sales levels. Determine the sales level (in millions of dollars) that is the cutoff between quarters that are considered "failures" by that company and quarters that are not. Carry your intermediate computations to at least four decimal places. Round your answer to one decimal place.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The sales level that is the cut-off between quarters that are considers as "failure" and those that are not is evaluated as

`y = 6.3 \ million \ dollars`

Explanation:

From the question we are told that the

Mean is
`\mu = 8 \ million \ dollars`

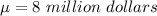
Standard deviation is
`\sigma = 1.3 \ million \ dollars`

Let Y be the random variable that denotes the sales made quarterly among health care information system

The normal distribution for this data is mathematically represented as

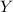`Y` ~ N
`(\mu = 8 , \sigma^2 = 1.69)`

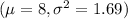
From the question we are told that a quarter is consider a failure by the company if the sales level that quarter in the bottom 10% of the of all quarterly sales

So

The the Probability of obtaining quarterly sales level that is equal to 10% of all quarterly sale (It is not below 10%) is mathematically represented as

`P[Y < y ] = 0.10`

This can be represented as a normal distribution in this manner

`P [ (Y- \mu)/(\sigma ) < (y -\mu)/(\sigma) ] = 0.10`

Where
`(Y - \mu )/(\sigma ) = Z` ~
`N(0 , 1)`

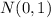
{This mean that this equal to the normal distribution between 0, 1 which is the generally range of every probability }

Therefor we have

`P[Z < (y- 8)/(1.3) ]`

The cumulative distribution function for a normal distribution of y is mathematically represented as

`\phi [(y- 8)/(1.3) ] = 0.10`

This is because a cumulative distribution function of a random value Y or a distribution of Y evaluated at y is the probability that Y will take will take a value that is less or equal to y

`(y- 8)/(1.3) = \phi ^(-1)(0.10)`

Calculating the inverse of the cumulative distribution function value of 0.10 which is negative the the critical value(Critical values determine what probability a particular variable will have when a sampling distribution is normal or close to normal.) of 0.01

`\phi ^(-1)(0.10) =- [1 - (0.10)/(2)]`

`= - 1.28155`

`(y - 8)/(1.3) = - 1.2816`

`=> y = 8 - (1.2816)(1.3)`

`y = 6.3 \ million \ dollars`