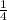Answer : The probability of getting a total that is a multiple of 4 is,
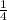
Step-by-step explanation :
Probability : It is defined as the extent to which an event is likely to occur. That means, it is measured by the ratio of the favorable outcomes to the total number of possible outcomes.
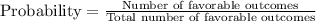
Favorable outcomes are:
(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
Favorable outcomes for getting a total that multiple of 4 are, (1,3), (2,2), (2,6), (3,1), (3,5), (4,4), (5,3), (6,2), (6,6)
Number of favorable outcomes for getting a total that multiple of 4 = 9
Total number of outcomes = 36
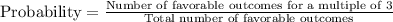
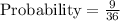
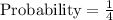
Therefore, the probability of getting a total that is a multiple of 4 is,