Question

Please Help!

Which equation is correct regarding the diagram of circle O?

m∠XZY = One-half(a + b)
m∠XZY = One-half(a – b)
m∠XOY = One-half(a + b)
m∠XOY = One-half(a – b)

Answer 1

B) m∠XZY = One-half(a – b)

Explanation:

Angles XOY and XZY add up to 180

b + XZY = 180

b = 180 - XZY

a + b = 360

½(a + b) = 180

b = ½(a + b) - XZY

XZY = ½(a + b) - b

XZY = ½a - ½b

XZY = ½(a - b)

Answer 2

Given:

Given that O is the center of the circle.

The lines XZ and YZ are the tangents of the circle.

The length of the major arc XY is a.

The length of the minor arc XY is b.

We need to determine the equation that is correct regarding the diagram.

Equation:

Since, we know the property, that "if the measure of an angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside the circle is equal to half the difference of the measures of the intercepted arcs."

Hence, applying the property, we get;

`m\angle XZY=(major \ arc \ XY - minor \ arc \ XY)/(2)`

Substituting the values, we get;

`m\angle XZY=(1)/(2)(a-b)`

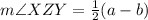
Therefore, the equation that is correct regarding the given diagram is
`m\angle XZY=(1)/(2)(a-b)`

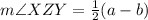
Hence, Option b is the correct answer.