Question

Using the data from Exercise 6.1.12 on cloud seeding, a. Find the median and quartiles for the unseeded cloud data. b. Find the median and quartiles for the seeded cloud data. c. Make two side-by-side box plots, one for each group on the same plot. d. Compare the distributions from what you can see in the side-by-side box plots.

Answer 1

Check below

Explanation:

a) Median and Quartiles for Unseeded Cloud

81.2 26.1 95 41.1 28.6 21.7 11.5 68.5 345.5 321.2 1202.6 1.0 4.9 163.0 372.4 244.3 47.3 87.0 26.3 24.4 830.1 4.9 36.6 147.8 17.3 29.0

1) Organizing it orderly:

1 4.9 4.9 11.5 17.3 21.7 24.4 26.1 26.3 28.6 29 36.6 41.1 47.3 68.5 81.2

87 95 147.8 163 244.3 321.2 345.5 372.4 830.1 1202.6

The Median is found by the adding the 26th and 27th value over two:

`Md=(26th+27th)/(2) =(41.1+47.3)/(2)=44.2`

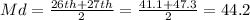
Md=Second Quartile=44.2

The First Quartile= 24.825

The Third Quartile=159.2

b) Find the median and quartiles for the seeded cloud data.

We'll proceed similarly let's check the data already orderly organized:

4.1 7.7 17.5 31.4 32.7 40.6 92.4 115.3 118.3 119 129.6 198.6 200.7 242.5

255 274.7 274.7 302.8 334.1 430 489.1 703.4 978 1656 1697.8 2745.6

The first quartile: 98.125

The second quartile (Median): 221.6

The Third Quartile: 406.025

c) Make two side-by-side box plots, one for each group on the same plot.

Check it below

Box plots

d). Compare the distributions from what you can see in the side-by-side box plots.

A Careful look will observe that much better results were obtained by the Seeded clouds.

A look at the values, quartiles, the upper limit and lower can clearly show that.

The Upper Quartile of the Unseed Clouds were not even close to the Seeded Cloud's first quartile.