Question

veryone's favorite flying sport disk can be approximated as the combination of a thin outer hoop and a uniform disk, both of diameter D d = 0.273 m. Dd=0.273 m. The mass of the hoop part is m h = 0.120 kg mh=0.120 kg and the mass of the disk part is m d = 0.050 kg. md=0.050 kg. Imagine making a boomerang that has the same total moment of inertia around its center as the sport disk. The boomerang is to be constructed in the shape of an "X," which can be approximated as two thin, uniform rods joined at their midpoints. If the total mass of the boomerang is to be m b = 0.255 kg, mb=0.255 kg, what must be the length L b Lb of the boomerang?

Answer 1

the length of the boomerang must be = 36.65 cm

Step-by-step explanation:

Given that:

diameter of both combination of a thin outer hoop and a uniform disk
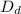`D _d` = 0.273 m

The mass of the hoop part is
`m _h` = 0.120 kg

The mass of the disk part is
`m _d` = 0.050 kg

The total mass of the boomerang is to be
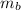`m _b` = 0.255 kg,

what must be the length
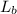`L _b` of the boomerang = ???

The moment of inertia of the sport disk is :

`{I = I_1} + I_2}`

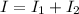
Let
`I_1}` be the moment of inertia of the hoop :

SO;
`I_1}`
`= m_h*r^2`

`I_1}`
`= 0.120*((0.273)/(2))^2`

`I_1}`
`= 0.120*(0.1365)^2`

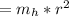
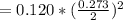
`I_1}` = 0.00223587 kgm²

Let
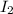`I_2}` be the moment of inertia of the disc

SO;
`I_2}`
`= (1)/(2)*m_d*r^2`

`I_2}`
`= (1)/(2)*0.050*((0.273)/(2))^2`

`I_2}`
`= 0.5*0.050*(0.1365)^2`

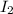
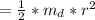
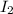
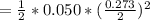
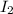
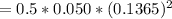
`I_2}` = = 0.0004658 kgm²

NOW;

`{I = I_1} + I_2}`

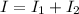
I = (0.00223587 + 0.0004658) kgm²

I = 0.00270167 kgm²

However; given that I is the moment of the boomerang

`{I = I_1} + I_2}`

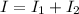
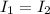`I_1} = I_2}` (i.e the moment of inertia in each rod )

`I = 2*I_1`

`0.00270167 = 2*(1)/(2)*\frac {0.255}{2}*lb^2\\\\\\0.00270167 = 0.02125 *lb^2\\\\lb^2 = (0.00270167)/(0.02125)\\\\ \\lb^2 = 0.1271\\\\lb = √(0.1271)\\\\lb = 0.3565 \ \ m\\\\lb = 36.65 \ \ cm`

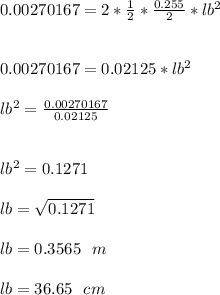
Therefore; the length of the boomerang must be = 36.65 cm