Question

A velocity selector is used to insert charged particles into a mas spectrometer at a specific speed. The velocity selector has uniform electric and magnetic fields that are perpendicular to one another and to the motion of the charged particle. If the particle is at the right velocity the magnetic force and electric force will cancel and the particle will continue in a straight line path. The velocity of the particle is: v=E/B. For higher or lower velocities, the particle is deflected and will not pass into the mass spectrometer.

Assuming the particle is positively charged, what are the directions of the forces due to the electric field and the magnetic field?

How does the kinetic energy of the particle change as it travels in the velocity selector?

Answer 1

please read the answer below

Step-by-step explanation:

A). If electric and magnetic forces over the charge allow that the particle describe a straight line, electric and magnetic forces are equal:

`F_E=F_B\\qE=qv\ X \ B`

electric and magnetic field are perpendicular between them and to the velocity of the charge, hence

v=E/B.

If the particle is moving to the right (+x), we can assume that electric field is upward (+z), and then magnetic field has a direction to out of the paper (+y). Thus, the electric force is directed upward (+z) and the cross product qv X B produces a magnetic force in the -z direction.

B).

`E_K=(1)/(2)mv^2=(1)/(2)m((E)/(B))^2`

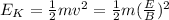
E and B are constant, hence, kinetic energy does not change.

hope this helps!