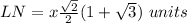Answer:
Part 1)
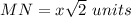
Part 2)
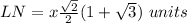
Explanation:
The picture of the question in the attached figure
step 1
Find the measure of ang;e M
Remember that the sum of the interior angles in any triangle must be equal to 180 degrees
so
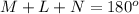
substitute the given values
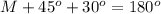
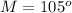
step 2
Applying the law of sines find the length side MN
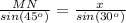
Remember that
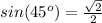
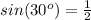
substitute
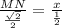
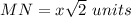
step 3
Find the length side LN
Construct the altitude from M to LN.
In the right triangle of the left
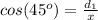 ---> by CAH (adjacent side divided by the hypotenuse)
---> by CAH (adjacent side divided by the hypotenuse)
Remember that
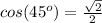
substitute
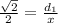
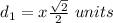
In the right triangle of the right
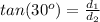 ---> by TOA (opposite side divided by adjacent side)
---> by TOA (opposite side divided by adjacent side)
Remember that
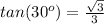
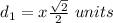
substitute
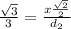
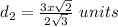
simplify
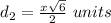
Find the length side LN
Remember that
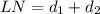
substitute the values
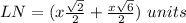
simplify