Question

Madame Pickney has a rather extensive art collection and the overall value of her collection has been increasing each year. Three years ago, her collection was worth $500,000. Two years ago, the value of the collection was $550,000 and last year, the collection was valued at $605,000.

Assume that the rate at which Madame Pickney’s art collection’s value increase remains the same as it has been for the last three years. The value of the art collection can be represented by a geometric sequence. The value of the collection three years ago is considered the first term in the sequence.
Write an explicit rule which can be used to determine the value of her art collection n years after that. Use this to determine the value of her collection 10 years after she started tracking its worth rounded to the nearest dollar.

PLEASE answer the value of her collections 10 years after she started tracking its worth.

Answer 1

Value = 500000 × (1.1^n)

$1,296,871

Explanation:

a = 500000

r = 550000 ÷ 500000 = 1.1

1st term is the initial year:

n years after that is the "n+1"th term

Value = 500000 × (1.1^n)

n = 10

500000(1.1¹⁰)

1,296,871.23005

Answer 2

About $1,178,974

Explanation:

Alright, the sequence we have right now is:

500,000 550,000 605,000

We want to find the common ratio, so let's divide 550,000 by 500,000 and see if we get the same value as 605,000 divided by 550,000:

550,000/500,000 = 1.1

605,000/550,000 = 1.1

Now, we know that r = 1.1. We also know the first term is:
`a_1` = 500,000.

We use the explicit rule of a geometric sequence:

`a_n=a_1*r^(n-1)`

Here, we want to find
`a_(10)` , which means that n = 10. We know r and
`a_1`, so we just plug in these values:

`a_(10)=500,000*(1.1)^(10-1)=500,000*(1.1)^(9)` ≈
`1,178,973.85` ≈
`1,178,974`

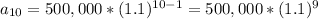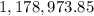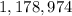
Thus, the answer is about $1,178,974.

Hope this helps!