Answer:
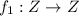 is one to one mapping, it is not onto mapping
is one to one mapping, it is not onto mapping
Explanation:
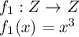
f₁(x) is one to one mapping
Let
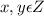
f₁(x) = f₁(y):
x₁³ = y₁³
f₁(x) is not onto mapping
Example: If f₁(x) = 7,
x₁³ = 7
![x_(1) = \sqrt[3]{7}](https://img.qammunity.org/2021/formulas/mathematics/college/df1qz85gtl240ircmk1tmsgobt7dju4lgb.png)
x₁ is not an element of Z
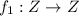 is one to one mapping, it is not onto mapping
is one to one mapping, it is not onto mapping