Answer:
Time period of second planet will be 126.40 days
Step-by-step explanation:
We have given radius of first planet

Orbital speed of first planet
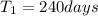
Radius of second planet
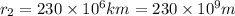
We have to find orbital period of second planet
Period of orbital is equal to
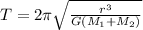
From the relation we can see that
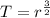
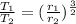
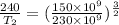
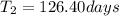
Time period of second planet will be 126.40 days