Question

(6) (Bonus) A rectangular box has its edges changing length as time passes. At a particular instant, the sides have lengths a = 150 feet, b = 80 feet, and c = 50 feet. At that instant, a is increasing at 100 feet/sec, b is decreasing 20 feet/sec, and c is increasing at 5 feet/sec. Determine if the volume of the box is increasing, decreasing, or not changing at all, at that instant.

Answer 1

Increasing,
`310000ft^3/s`

Explanation:

We are given that

a=150 feet

b=80 feet

c=50 feet

`(da)/(dt)=100ft/s`

`(db)/(dt)=-20ft/s`

`(dc)/(dt)=5ft/s`

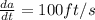
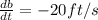
We have to find the volume of the box of the box increasing,decreasing or not changing at all at that instant.

We know that

Volume of box=
`lbh`

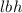
Using the formula

Volume of box,V=abc

Differentiate w.r.t t

`(dV)/(dt)=(da)/(dt)bc+(db)/(dt)(ac)+(dc)/(dt)(ab)`

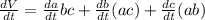
Substitute the values

`(dV)/(dt)=100(80* 50)-20(150* 50)+5(150* 80)`

`(dV)/(dt)=310000ft^3/s`

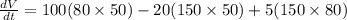
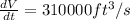
Hence, the volume of the box is increasing .