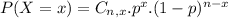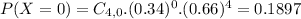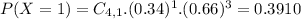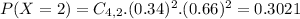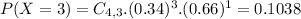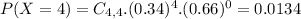Question

Some parts of California are particularly earthquake-prone. Suppose that in one metropolitan area, the chance a homeowner is insured against an earthquake is 0.34. A sample of four homeowners are to be selected at random. Suppose X is a random variable that is modeled by a binomial distribution which describes the number of homeowners out of the four that have earthquake insurance.

(a) Find the probability mass function of X. (Round your answers to four decimal places.)

Answer 1

The probability mass function would be:

`P(X) = (4Cx) (0.34)^x (1-0.34)^(4-x) , x=0,1,2,3,4`

And replacing the values of x we have:

`P(X=0)=(4C0) (0.34)^0 (1-0.34)^(4-0) =0.1897`

`P(X=1)=(4C1) (0.34)^1 (1-0.34)^(4-1) =0.3910`

`P(X=2)=(4C2) (0.34)^2 (1-0.34)^(4-2) =0.3021`

`P(X=3)=(4C3) (0.34)^3 (1-0.34)^(4-3) =0.1038`

`P(X=4)=(4C4) (0.34)^4 (1-0.34)^(4-4) =0.0134`

Explanation:

Previous concepts

The binomial distribution is a "DISCRETE probability distribution that summarizes the probability that a value will take one of two independent values under a given set of parameters. The assumptions for the binomial distribution are that there is only one outcome for each trial, each trial has the same probability of success, and each trial is mutually exclusive, or independent of each other".

Solution to the problem

Let X the random variable of interest "number of homeowners out of the 4 that have earthquake insurance", on this case we now that:

`X \sim Binom(n=4, p=0.34)`

The probability mass function for the Binomial distribution is given as:

`P(X)=(nCx)(p)^x (1-p)^(n-x)`

Where (nCx) means combinatory and it's given by this formula:

`nCx=(n!)/((n-x)! x!)`

Part a

The probability mass function would be:

`P(X) = (4Cx) (0.34)^x (1-0.34)^(4-x) , x=0,1,2,3,4`

And replacing the values of x we have:

`P(X=0)=(4C0) (0.34)^0 (1-0.34)^(4-0) =0.1897`

`P(X=1)=(4C1) (0.34)^1 (1-0.34)^(4-1) =0.3910`

`P(X=2)=(4C2) (0.34)^2 (1-0.34)^(4-2) =0.3021`

`P(X=3)=(4C3) (0.34)^3 (1-0.34)^(4-3) =0.1038`

`P(X=4)=(4C4) (0.34)^4 (1-0.34)^(4-4) =0.0134`

Answer 2

P(X = 0) = 0.1897

P(X = 1) = 0.3910

P(X = 2) = 0.3021

P(X = 3) = 0.1038

P(X = 4) = 0.0134

Explanation:

For each owner, there are only two possible outcomes. Either they are insured against an earthquake, or they are not. The probability of a homeowner being insured against an earthquake is independent of other homeowners. So the binomial probability distribution is used to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

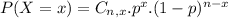
In which
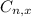`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

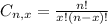
And p is the probability of X happening.

Suppose that in one metropolitan area, the chance a homeowner is insured against an earthquake is 0.34.

This means that
`p = 0.34`

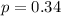
A sample of four homeowners are to be selected at random.

This means that
`n = 4`

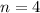
(a) Find the probability mass function of X. (Round your answers to four decimal places.)

The pmf is the probability of each outcome.

So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(4,0).(0.34)^(0).(0.66)^(4) = 0.1897`

`P(X = 1) = C_(4,1).(0.34)^(1).(0.66)^(3) = 0.3910`

`P(X = 2) = C_(4,2).(0.34)^(2).(0.66)^(2) = 0.3021`

`P(X = 3) = C_(4,3).(0.34)^(3).(0.66)^(1) = 0.1038`

`P(X = 4) = C_(4,4).(0.34)^(4).(0.66)^(0) = 0.0134`