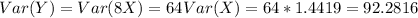Answer:
a)
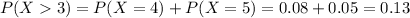
b)
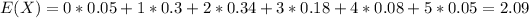
Now in order to calculate the variance we need to calculate the second moment given by:
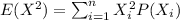
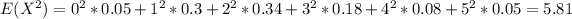
And the variance would be given by:
![Var(X) = E(X^2) -[E(X)]^2 = 5.81 -(2.09)^2 =1.4419](https://img.qammunity.org/2021/formulas/mathematics/college/f1jng5qwm52t5n05667s2z7s45j5zwb7wt.png)
c)
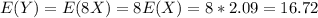
d)
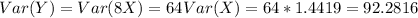
Explanation:
Previous concepts
In statistics and probability analysis, the expected value "is calculated by multiplying each of the possible outcomes by the likelihood each outcome will occur and then summing all of those values".
The variance of a random variable Var(X) is the expected value of the squared deviation from the mean of X, E(X).
And the standard deviation of a random variable X is just the square root of the variance.
Solution to the problem
For this case we define the random variable X as "number of times a certain computer program will malfunction" and we have the following distribution function for X
X 0 1 2 3 4 5
P(X) 0.05 0.3 0.34 0.18 0.08 0.05
Part a
For this case we want this probability:
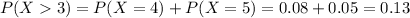
Part b
We can calculate the expected value with this formula:
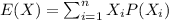
And replacing we got:
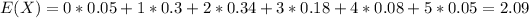
Now in order to calculate the variance we need to calculate the second moment given by:
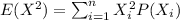
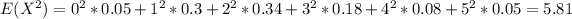
And the variance would be given by:
![Var(X) = E(X^2) -[E(X)]^2 = 5.81 -(2.09)^2 =1.4419](https://img.qammunity.org/2021/formulas/mathematics/college/f1jng5qwm52t5n05667s2z7s45j5zwb7wt.png)
Part c
For this case we define this new random variable Y = 8X
The expected value is given by:
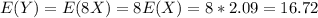
Part d
The variance would be given by: