Question

Joe heard from a reliable source that only 22% of people actually sleep 8 hours or more per night. You do a survey and find 58 out of 148 sleep for 8 hours or longer. Build a 95% confidence interval. Round to the nearest hundredth.

Answer 1

95% Confidence interval: (31.32%,47.04%)

Explanation:

We are given the following in the question:

Sample size, n = 148

Number of people who sleep for 8 hours or longer, x = 58

`\hat{p} = (x)/(n) = (58)/(148) = 0.3918`

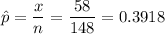
95% Confidence interval:

`\hat{p}\pm z_(stat)\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

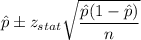
Putting the values, we get:

`0.3918\pm 1.96(\sqrt{(0.3918(1-0.3918))/(148)})\\\\ = 0.3918\pm 0.0786\\\\=(0.3132,0.4704)=(31.32\%,47.04\%)`

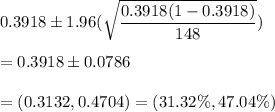
(31.32%,47.04%) is the required 95% confidence interval.