Question

To practice Problem-Solving Strategy 6.1 Work and Kinetic Energy. Your cat Goldie (mass 8.50 kg ) is trying to make it to the top of a frictionless ramp 39.930 m long and inclined 27.0 ∘ above the horizontal. Since Goldie can’t get any traction on the ramp, you push her up the entire length of the ramp by exerting a constant 37.40 N force parallel to the ramp (there is a set of stairs alongside the frictionless ramp on which you can walk). If Goldie is moving at 2.000 m/s at the bottom of the ramp (assume she has gotten a running start), what is her speed when she reaches the top of the incline?

Answer 1

Step-by-step explanation:

the forces parallel to the ramp are:

`F-F_g=ma\\F-mgsin\theta=ma`

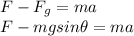
where F is the force exerted by the person, Mg is the weight of the cat, theta is the angle of the ramp, m is the mass of the cat and a is the acceleration.

By replacing we can obtain the acceleration of the cat:

`a=((37.40N)-(8.50kg)(9.8(m)/(s^2))(sin27\°))/(8.50kg)=-0.417(m)/(s^2)`

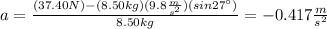
Then, the cat is slowing down while it is going up the ramp.

Now, we can compute the final speed by using the following formula:

`v^2=v_0^2+2ad\\\\v=√(v_0^2+2gd)=√((2.0m/s)^2+2(-0.417m/s^2)(39.930m))`

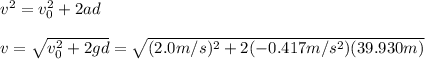
!!! the cat has a negative acceleration, hence, the force exerted by the person is not enough to move the cat upward.

it is neccesary to review the values of the exercise