Question

Pleaseeee helpppp me


What is the perimeter of ABDE

Answer 1

Given:

Given that the graph of a triangle BDE.

The coordinates of the triangle are B(-2,3), D(2,6) and E(3,2)

We need to determine the perimeter of the triangle BDE.

Length of BD:

The length of BD can be determined by substituting the coordinates (-2,3) and (2,6) in the formula,

`BD=√((x_2-x_1)^2+(y_2-y_1)^2)`

`BD=√((2+2)^2+(6-3)^2)`

`BD=√((4)^2+(3)^2)`

`BD=√(16+9)`

`BD=√(25)`

`BD=5`

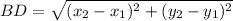
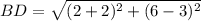
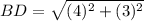
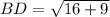
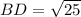
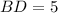
Length of DE:

Substituting the coordinates of D(2,6) and E(3,2) in the formula, we get;

`DE=√((3-2)^2+(2-6)^2)`

`DE=√((1)^2+(-4)^2)`

`DE=√(1+16)`

`DE=√(17)`

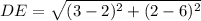
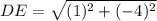
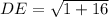
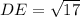
Length of BE:

Substituting the coordinates of B(-2,3) and E(3,2) in the formula, we get;

`BE=√((3+2)^2+(2-3)^2)`

`BE=√((5)^2+(-1)^2)`

`BE=√(25+1)`

`BE=√(26)`

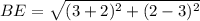
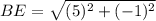
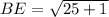
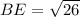
Perimeter of ΔBDE:

The perimeter of triangle BDE can be determined by adding the lengths of BD, DE and BE.

Thus, we have;

`Perimeter=5+√(17)+√(26)`

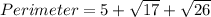
Hence, the perimeter of ΔBDE is √17 + √26 + 5

Thus, Option A is the correct answer.