Question

Determine the pH during the titration of 23.5 mL of 0.346 M formic acid (Ka = 1.8×10-4) by 0.457 M KOH at the following points.

(a) Before the addition of any KOH
(b) After the addition of 4.00 mL of KOH
(c) At the half-equivalence point (the titration midpoint)
(d) At the equivalence point
(e) After the addition of 26.7 mL of KOH

Answer 1

(a) pH=2.11; (b) pH=2.20; (c) pH=3.75; (d) pH=8.52 y (e) pH=12.91

Step-by-step explanation:

To find the pH of the different points we will use the following equation:

`pH = -log([H_(3)O^(+)])` (1)

(a) The reaction of the formic acid before the addition of any KOH is:

CHOOH + H₂O ⇆ CHOO⁻ + H₃O⁺ (2)

0.346 M

0.346 - x x x

The dissociation constant of the formic acid is:

`K_(a) = ([CHOO^(-)][H_(3)O^(+)])/([CHOOH])` (3)

`K_(a) = (x^(2))/(0.346 - x)`

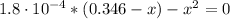`1.8 \cdot 10^(-4)*(0.346 - x) - x^(2) = 0` (4)

Solving equation (4) for x:

x = [CHOO⁻] = [H₃O⁺] = 0.0078

Hence, the pH before the addition of any KOH is:

`pH = -log(0.0078) = 2.11`

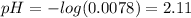
(b) After the addition of 4.00 mL of KOH we have the following equation:

CHOOH + OH⁻ ⇆ CHOO⁻ + H₂O (5)

The number of moles of the formic acid and KOH is:

`\eta_(CHOOH) = C*V = 0.346 M*23.5 \cdot 10^(-3) L = 8.13 \cdot 10^(-3) moles`

`\eta_(KOH) = C*V = 0.457 M*4 \cdot 10^(-3) L = 1.83 \cdot 10^(-3) moles`

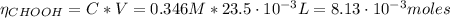
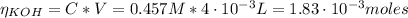
Now, from the reaction of equation (5) we have the following number of moles of acid:

`\eta_(CHOOH) - \eta_(KOH) = 8.13 \cdot 10^(-3) moles - 1.83 \cdot 10^(-3) moles = 6.30 \cdot 10^(-3) moles`

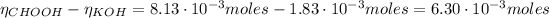
The concentration of the formic acid is:

`C_(CHOOH) = (\eta_(CHOOH))/(V_(T)) = (6.30 \cdot 10^(-3) moles)/((23.5 \cdto 10^(-3) L + 4.00 \cdot 10^(-3) L)) = 0.23 M`

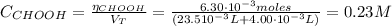
From the reaction of dissociation of the formic acid (equation 2) and using equation (3), we can find the pH:

`K_(a) = ([CHOO^(-)][H_(3)O^(+)])/([CHOOH])`

`K_(a) = (x^(2))/(0.23 - x)`

`1.8 \cdot 10^(-4)*(0.23 - x) - x^(2) = 0`

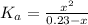
By solving the above equation for x, we have:

x = [CHOO⁻] = [H₃O⁺] = 0.0063

Hence, the pH after the addition of 4.00 mL of KOH is:

`pH = -log(0.0063) = 2.20`

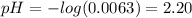
(c) At the half-equivalence point (the titration midpoint) we have that the KOH converted half of the CHOOH into its conjugate base CHOO⁻, so the pH of the solution is given by the Henderson-Hasselbalch equation:

`pH = pKa + log(([CHOO^(-)])/([CHOOH]))`

`pH = -log(1.8 \cdot 10^(-4)) + log((\eta_(CHOO^(-))/V_(T))/(\eta_(CHOOH)/V_(T)))`

`pH = -log(1.8 \cdot 10^(-4)) + log((\eta_(CHOO^(-)))/(\eta_(CHOOH)))`

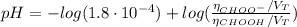
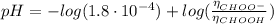
Since the number of moles of the acid is equal to the number of moles of its conjugate base CHOO⁻ (by definition of the half-equivalence point), we have:

`pH = -log(1.8 \cdot 10^(-4)) + log(1) = 3.75`

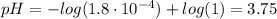
Hence, the pH at the half-equivalence point is given by the dissociation constant of the acid = 3.75.

(d) At the equivalence point, the number of moles of the formic acid is equal to the number of moles of KOH, so they neutralize. The conjugate base of the formic acid (CHOO⁻) will react with H₂O to produce OH⁻ ions:

CHOOH + OH⁻ ⇆ CHOO⁻ + H₂O

8.13x10⁻³ moles 8.13x10⁻³ moles

0 0 8.13x10⁻³ moles

The concentration of the CHOO⁻ is:

`C = (\eta_(CHOO^(-)))/(V_(T)) = (\eta_(CHOO^(-)))/(\eta_(KOH)/C_(KOH) + Va) = (8.13 \cdot 10^(-3) moles)/((8.13 \cdot 10^(-3) moles)/(0.457 M) + 23.5 \cdot 10^(-3) L) = 0.20 M`

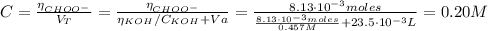
CHOO⁻ + H₂O ⇆ CHOOH + OH⁻ (6)

0.20 - x x x

The dissociation constant of equation (6) is:

`K_(b) = ([CHOOH][OH^(-)])/([CHOO^(-)])`

Since Ka*Kb = Kw = 1.0x10⁻¹⁴ we have:

`(K_(w))/(K_(a)) = ([CHOOH][OH^(-)])/([CHOO^(-)])`

`(1.0 \cdot 10^(-14))/(1.8 \cdot 10^(-4)) = (x^(2))/(0.20 - x)`

`5.56 \cdot 10^(-11)*(0.20 - x) - x^(2) = 0`

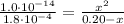
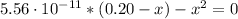
Solving the above equation for x:

x = [CHOOH] = [OH⁻] = 3.34x10⁻⁶ M

Therefore, the pH at the equivalence point is:

`pH = 14 - pOH = 14 - (-log(3.34 \cdot 10^(-6))) = 8.52`

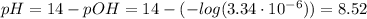
(e) After the addition of 26.7 mL of KOH, we have that the pH is given by the KOH. The moles of the KOH is:

`\eta_(KOH) = \eta_(KOH) - \eta_(CHOOH) = 0.457 M*26.7 \cdot 10^(-3) L - 0.346 M*23.5 \cdot 10^(-3) L = 4.07 \cdot 10^(-3) moles`

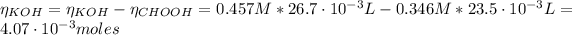
Now, the concentration of the KOH is:

`C = (\eta)/(V_(T)) = (4.07 \cdot 10^(-3) moles)/(50.2 \cdot 10^(-3) L) = 0.081 M`

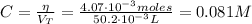
Finally, the pH after the addition of 26.7 mL of KOH is:

`pH = 14 - pOH = 14 - (-log(0.081)) = 12.91`

I hope it helps you!