Answer:
a) The mean of the sampling proportion is p=0.25. The standard deviation is σ=0.016. The shape is like a bell.
b) I wouldn't be surprised as there is a 10% chance of getting this value p=0.27 or more for a sample proportion.
c) This sample proportion p=0.31 has a null probability of happening, so I would be surprised of getting that value.
Explanation:
The question is incomplete:
a) Describe the sampling distribution (shape, center and spread) of p for a sample size of n=728, if the null hypothesis is true (p=0.25).
b) Would you be surprised to observe a sample proportion p=0.27 for a sample size of n=728 if the null hypothesis (p=0.25) is true?
c) Would you be surprised to observe a sample proportion p=0.31 for a sample size of n=728 if the null hypothesis (p=0.25) is true?
a) The sampling distribution would be centered in the null hypothesis proportion (p-0.25). Then, the mean of the sampling proportion is p=0.25.
The standard deviation would be:
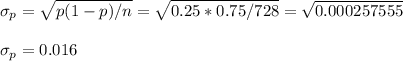
As it would be a binomial-like distribution, the shape will be a bell-shape.
b) We can calculate the likelyhood of a value p=0.27 in this distribution calculating the z-value and looking for its probability in the standard normal distribution.
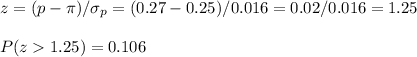
I wouldn't be surprised as there is a 10% chance of getting this value p=0.27 or more for a sample proportion.
c) We repeat the calculation for p=0.31
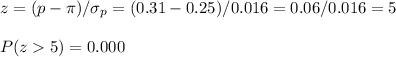
This sample proportion p=0.31 has a null probability of happening, so I would be surprised of getting that value.