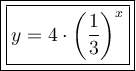Answer:
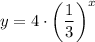
Explanation:
The general form of an exponential function is:

The y-intercept is the point at which a graph intersects the y-axis, so where the x-coordinate is zero. Therefore, to find the initial value (a) from the given table of values, identify the y-value that corresponds to x = 0. So:

As the x-values in the table increase by a constant value of one, to find the base (b) of the exponential function, we divide a y-value by the preceding y-value:
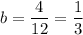
Therefore, the equation of the exponential function that models the given table of values is: