Answer:
a) 25
b) 67
c) 97
Explanation:
We have that to find our
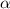 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
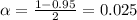
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
So it is z with a pvalue of
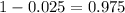 , so
, so
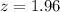
Now, find the margin of error M as such
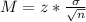
In which
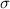 is the standard deviation of the population and n is the size of the sample. In this problem,
is the standard deviation of the population and n is the size of the sample. In this problem,
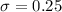
(a) The desired margin of error is $0.10.
This is n when M = 0.1. So
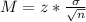
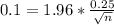
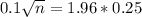
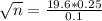
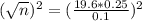
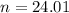
Rounding up to the nearest whole number, 25.
(b) The desired margin of error is $0.06.
This is n when M = 0.06. So
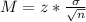
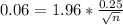
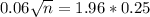
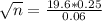
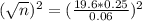
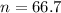
Rounding up, 67
(c) The desired margin of error is $0.05.
This is n when M = 0.05. So
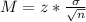
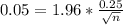
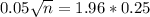
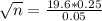
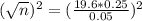
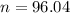
Rounding up, 97