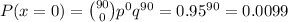Question

NBC News reported on May 2, 2013, that 1 in 20 children in the United States have a food allergy of some sort. Consider selecting a random sample of 15 children and let X be the number in the sample who have a food allergy. Then X ~ Bin(15, 0.05). (Round your probabilities to three decimal places.) (a) Determine both P(X ≤ 3) and P(X < 3). P(X ≤ 3) = P(X < 3) = (b) Determine P(X ≥ 4). P(X ≥ 4) = (c) Determine P(1 ≤ X ≤ 3). P(1 ≤ X ≤ 3) = (d) What are E(X) and σX? (Round your answers to two decimal places.) E(X) = σX = (e) In a sample of 90 children, what is the probability that none has a food allergy?

Answer 1

a) P(X ≤ 3) = 0.9946

P(X < 3) = 0.9639

b) P(X ≥ 4) = 0.0054

c) P(1 ≤ X ≤ 3) = 0.5313

d) E(X) = 0.75

σX = 0.84

e) P(X=0) = 0.0099

Explanation:

We have x: number in the sample who have a food allergy. As the sample is of n=15 and p=0.05, we have:

`X \sim Bin(15, 0.05)`

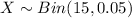
a) We have to determine P(X ≤ 3) and P(X < 3)

We can calculate P(X ≤ 3) as the sum of P(0), P(1), P(2) and P(3).

`P(x\leq 3)=\sum_(k=0)^3P(k)\\\\\\P(x=0) = \binom{15}{0} p^(0)q^(15)=1*1*0.4633=0.4633\\\\P(x=1) = \binom{15}{1} p^(1)q^(14)=15*0.05*0.4877=0.3658\\\\P(x=2) = \binom{15}{2} p^(2)q^(13)=105*0.0025*0.5133=0.1348\\\\P(x=3) = \binom{15}{3} p^(3)q^(12)=455*0.0001*0.5404=0.0307\\\\\\P(x\leq 3)=0.4633+0.3658+0.1348+0.0307=0.9946`

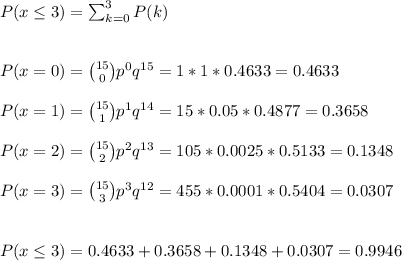
P(x<3) can be calculated from the previos result as:

`P(x<3)=P(X\leq3)-P(3)=0.9946-0.0307=0.9639`

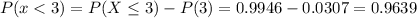
b) We can calculate P(X ≥ 4) as:

`P(X\geq4)=1-P(X<4)=1-P(X\leq3)=1-0.9946=0.0054`

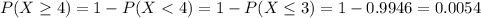
c) We can calculate P(1 ≤ X ≤ 3) as:

`P(1 \leq X \leq 3)=P(1)+P(2)+P(3)=0.3658+0.1348+0.0307=0.5313`

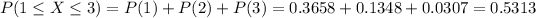
d) The expected value of a binomial variable is the product of the sample size n and the probability of success p:

`E(X)=np=15*0.05=0.75`

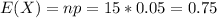
The standard deviation is calculates as:

`\sigma_x=√(np(1-p))=√(15*0.05*0.95)=√(0.7125) =0.84`

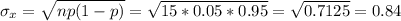
e) In this case, the sample size is n=90.

We can calculate the probability that none has a food allergy as:

`P(x=0) = \binom{90}{0} p^(0)q^(90)=0.95^(90)=0.0099`